Risk Management and Portfolio Optimization

In this topic, we'll delve into the world of risk management and portfolio optimization using Python. From understanding the basics of risk in investments to implementing advanced optimization techniques, we'll explore how Python can be leveraged to construct optimal investment portfolios tailored to individual objectives and constraints. Let's embark on a journey to master the art of risk management and portfolio optimization in Python.

Introduction to Risk Management

Understanding Risk in Investments

Risk in investments refers to the uncertainty of returns and the possibility of financial loss. Investors face various types of risks, including market risk, credit risk, liquidity risk, and operational risk.

Importance of Risk Management

Risk management is crucial for investors to protect their capital and achieve their financial goals. Effective risk management strategies help investors minimize potential losses and maximize returns, thereby enhancing the overall performance of their investment portfolios.

Basic Concepts of Portfolio Optimization

What is Portfolio Optimization?

Portfolio optimization is the process of constructing an investment portfolio that maximizes returns while minimizing risk. It involves selecting the optimal combination of assets to achieve the desired risk-return profile based on the investor’s objectives and constraints.

Key Metrics in Portfolio Optimization

Expected Return: The average return expected from an investment portfolio over a specified period.
Risk (Volatility): The measure of uncertainty or variability of returns associated with an investment portfolio.
Sharpe Ratio: A risk-adjusted measure that evaluates the performance of an investment portfolio relative to its risk.

Modern Portfolio Theory (MPT)

Introduction to Modern Portfolio Theory

Modern Portfolio Theory (MPT), proposed by Harry Markowitz, is a framework for portfolio construction based on the principles of diversification and risk-return tradeoff. MPT aims to maximize portfolio returns for a given level of risk or minimize risk for a given level of return.

The Efficient Frontier

The efficient frontier represents a set of optimal portfolios that offer the highest expected return for a given level of risk or the lowest risk for a given level of return. It illustrates the tradeoff between risk and return and helps investors identify the optimal portfolio allocation.

Portfolio Optimization Techniques

Mean-Variance Optimization

Mean-Variance Optimization (MVO) is a classical approach to portfolio optimization that aims to maximize the expected return of a portfolio while minimizing its volatility. It involves calculating the expected return, volatility, and covariance of assets to construct an efficient portfolio.

Example of Mean-Variance Optimization

				
					# Python code example for Mean-Variance Optimization
import numpy as np
from scipy.optimize import minimize

# Define expected returns and covariance matrix
expected_returns = np.array([0.1, 0.15, 0.2])
covariance_matrix = np.array([[0.1, 0.05, 0.03],
                               [0.05, 0.12, 0.08],
                               [0.03, 0.08, 0.15]])

# Define objective function (negative Sharpe ratio)
def negative_sharpe(weights):
    portfolio_return = np.dot(weights, expected_returns)
    portfolio_std_dev = np.sqrt(np.dot(weights.T, np.dot(covariance_matrix, weights)))
    sharpe_ratio = portfolio_return / portfolio_std_dev
    return -sharpe_ratio

# Define constraints (sum of weights equals 1)
constraints = ({'type': 'eq', 'fun': lambda weights: np.sum(weights) - 1})

# Define bounds (weights between 0 and 1)
bounds = tuple((0, 1) for _ in range(len(expected_returns)))

# Initial guess for weights
initial_guess = np.ones(len(expected_returns)) / len(expected_returns)

# Optimize portfolio weights
result = minimize(negative_sharpe, initial_guess, method='SLSQP', bounds=bounds, constraints=constraints)

# Display optimized portfolio weights
print("Optimized Portfolio Weights:", result.x)

Explanation:

In this example, we use Python and the SciPy library to perform Mean-Variance Optimization (MVO) for portfolio optimization.
We define the expected returns of assets and the covariance matrix of asset returns.
We define the objective function as the negative Sharpe ratio, which we aim to minimize.
We set constraints on the sum of weights to ensure that they add up to 1.
We specify bounds for the weights to ensure they are between 0 and 1.
Finally, we use the minimize function to optimize the portfolio weights and display the optimized weights.

Advanced Portfolio Optimization Techniques

Black-Litterman Model

The Black-Litterman Model is an advanced portfolio optimization technique that combines the views of investors with market equilibrium to generate optimal portfolio allocations. It allows investors to incorporate subjective views and beliefs into the portfolio optimization process.

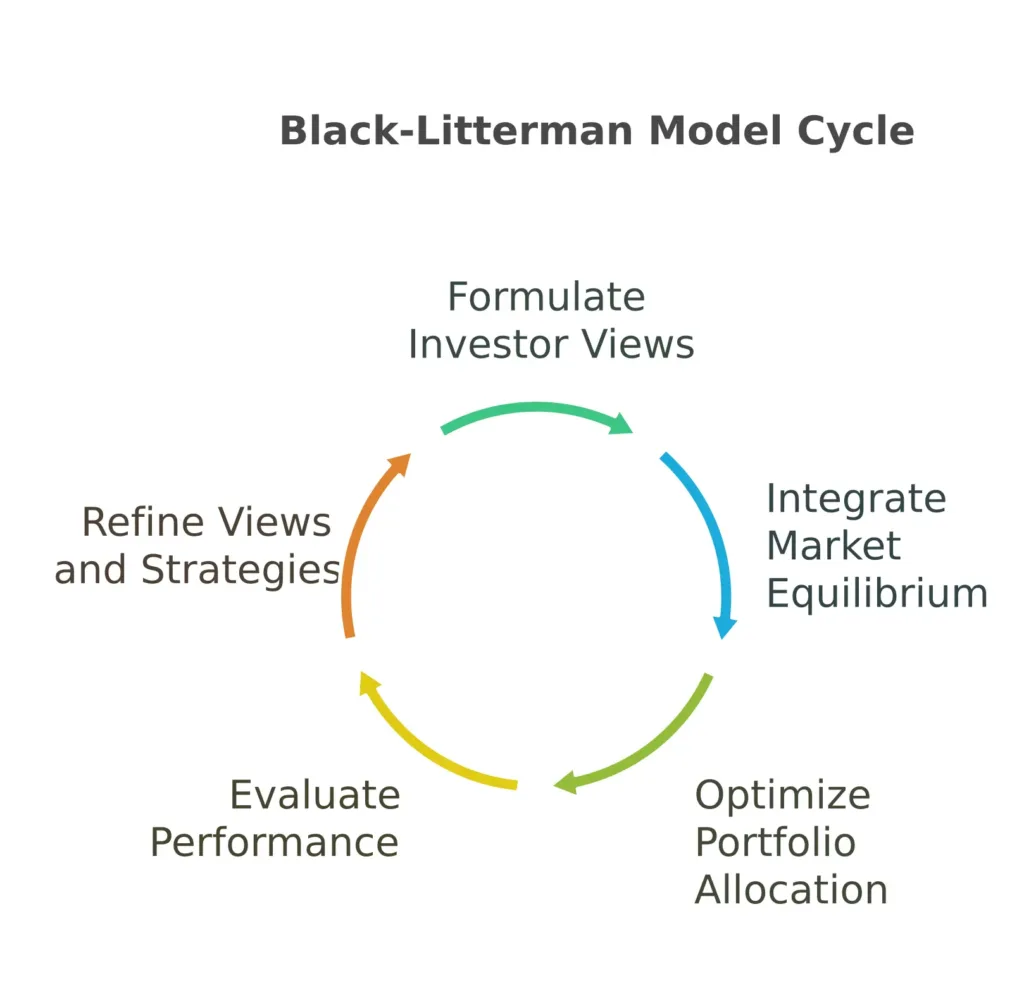
Formulate Investor Views

Start with subjective views: Investors provide opinions or expectations about the performance of assets. These views can be:
- Absolute Views: E.g., “Asset A will return 6%.”
- Relative Views: E.g., “Asset A will outperform Asset B by 2%.”
Quantify the confidence level: Each view is assigned a degree of certainty (from very confident to less confident) to balance it against market equilibrium.

Integrate Market Equilibrium

The market equilibrium reflects the consensus view of all market participants, derived from market data.
- Use market-capitalization weights of assets to infer their implied expected returns (reverse optimization).
These equilibrium returns serve as a baseline for blending with investor views.

Optimize Portfolio Allocation

Combine the market equilibrium returns with the investor views using Bayesian inference.
The result is a set of adjusted expected returns that:
- Incorporate investor views proportionate to their confidence levels.
- Maintain the diversification benefits of market equilibrium.
Perform mean-variance optimization to calculate the optimal portfolio allocation based on the adjusted returns.

Evaluate Performance

After constructing the portfolio, monitor its performance against benchmarks and expectations.
- Assess whether the portfolio meets the risk-return trade-offs defined during optimization.
- Compare the realized returns against both market equilibrium and investor expectations.

Refine Views and Strategies

Based on performance evaluation, refine the inputs for the model:
- Adjust confidence levels in views.
- Update views based on new information or market changes.
- Reassess the weight of market equilibrium if views prove more reliable.

Repeat: Formulate Investor Views

Begin the cycle again by incorporating the updated insights into a new set of investor views.
This iterative process ensures the portfolio stays aligned with evolving market conditions and investor strategies.

In the above topic, we've explored the principles and techniques of risk management and portfolio optimization in Python. From understanding basic concepts such as risk and return to advanced optimization techniques like Mean-Variance Optimization and the Black-Litterman Model, investors can leverage Python's powerful libraries and tools to construct optimal investment portfolios tailored to their objectives and constraints. By mastering these techniques, investors can enhance their portfolio performance, mitigate risks, and achieve their financial goals effectively. Happy coding! ❤️