Trees in Go

Trees are hierarchical data structures widely used in computer science and programming. In Go, trees play a vital role in various applications, ranging from organizing data efficiently to implementing search algorithms. This chapter explores trees in detail, from basic concepts to advanced techniques, with comprehensive examples and explanations.

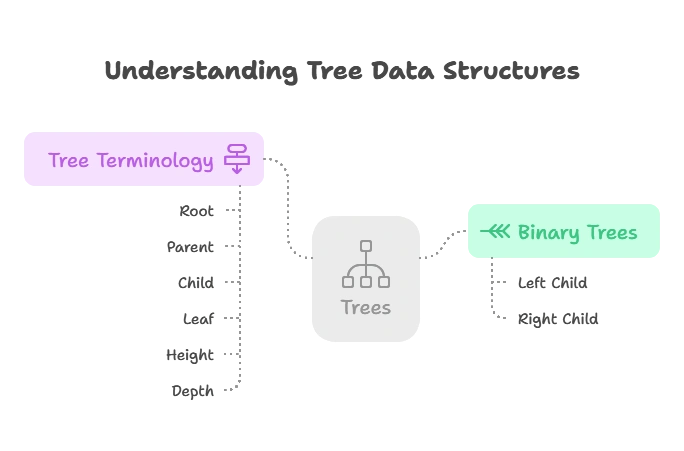
What are Trees?

Trees are nonlinear data structures composed of nodes connected by edges. Each node contains data and may link to other nodes, forming a hierarchical structure with a root node at the top.

Binary Trees

Binary trees are trees where each node has at most two children: a left child and a right child. They are fundamental in computer science and serve as the basis for many other tree-based data structures.

Tree Terminology

Root: The topmost node in a tree.
Parent: A node that has one or more child nodes.
Child: A node directly connected to another node when moving away from the root.
Leaf: A node with no children.
Height: The length of the longest path from the root to a leaf.
Depth: The length of the path from the root to a particular node.

Types of Trees

Binary Search Trees (BST)

Binary Search Trees are a type of binary tree where the left subtree contains nodes with keys less than the root node’s key and the right subtree contains nodes with keys greater than the root node’s key. This property makes search, insertion, and deletion operations efficient.

AVL Trees

AVL trees are self-balancing binary search trees where the height difference between the left and right subtrees of any node is at most one. This property ensures balanced trees, leading to faster search and insertion operations.

Red-Black Trees

Red-Black trees are another type of self-balancing binary search trees. They ensure balance by applying specific rules during insertion and deletion operations, guaranteeing logarithmic time complexity for search, insertion, and deletion.

Heap

A heap is a specialized tree-based data structure that satisfies the heap property. In a min heap, the parent node is smaller than or equal to its children, while in a max heap, the parent node is larger than or equal to its children. Heaps are commonly used to implement priority queues.

Trie (Prefix Tree)

Implementations and Examples

Binary Tree

				
					package main

import "fmt"

type TreeNode struct {
    Data  int
    Left  *TreeNode
    Right *TreeNode
}

func main() {
    // Creating a binary tree
    root := &TreeNode{Data: 1}
    root.Left = &TreeNode{Data: 2}
    root.Right = &TreeNode{Data: 3}
    root.Left.Left = &TreeNode{Data: 4}
    root.Left.Right = &TreeNode{Data: 5}

    // Print the binary tree
    fmt.Println("Binary Tree:")
    printTree(root)
}

func printTree(node *TreeNode) {
    if node == nil {
        return
    }
    fmt.Println(node.Data)
    printTree(node.Left)
    printTree(node.Right)
}

We define a TreeNode struct representing each node in the binary tree.
In the main function, we create a binary tree by linking nodes together.
The printTree function recursively prints the data of each node in the tree.

Binary Search Tree (BST)

				
					package main

import "fmt"

type TreeNode struct {
    Data  int
    Left  *TreeNode
    Right *TreeNode
}

func main() {
    // Creating a BST
    root := insert(nil, 4)
    insert(root, 2)
    insert(root, 6)
    insert(root, 1)
    insert(root, 3)
    insert(root, 5)
    insert(root, 7)

    // Print the BST
    fmt.Println("Binary Search Tree:")
    printInOrder(root)
}

func insert(root *TreeNode, data int) *TreeNode {
    if root == nil {
        return &TreeNode{Data: data}
    }
    if data < root.Data {
        root.Left = insert(root.Left, data)
    } else if data > root.Data {
        root.Right = insert(root.Right, data)
    }
    return root
}

func printInOrder(node *TreeNode) {
    if node == nil {
        return
    }
    printInOrder(node.Left)
    fmt.Println(node.Data)
    printInOrder(node.Right)
}

We define a TreeNode struct representing each node in the binary search tree (BST).
In the main function, we insert elements into the BST using the insert function.
The insert function recursively inserts elements according to the BST property.
We print the BST using the printInOrder function, which performs an in-order traversal to print the elements in sorted order.

AVL Tree

				
					package main

import "fmt"

type AVLNode struct {
    Data   int
    Height int
    Left   *AVLNode
    Right  *AVLNode
}

func height(node *AVLNode) int {
    if node == nil {
        return 0
    }
    return node.Height
}

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

func rotateRight(y *AVLNode) *AVLNode {
    x := y.Left
    T2 := x.Right

    x.Right = y
    y.Left = T2

    y.Height = max(height(y.Left), height(y.Right)) + 1
    x.Height = max(height(x.Left), height(x.Right)) + 1

    return x
}

func rotateLeft(x *AVLNode) *AVLNode {
    y := x.Right
    T2 := y.Left

    y.Left = x
    x.Right = T2

    x.Height = max(height(x.Left), height(x.Right)) + 1
    y.Height = max(height(y.Left), height(y.Right)) + 1

    return y
}

func getBalance(node *AVLNode) int {
    if node == nil {
        return 0
    }
    return height(node.Left) - height(node.Right)
}

func insert(root *AVLNode, data int) *AVLNode {
    if root == nil {
        return &AVLNode{Data: data, Height: 1}
    }

    if data < root.Data {
        root.Left = insert(root.Left, data)
    } else if data > root.Data {
        root.Right = insert(root.Right, data)
    } else {
        return root // Duplicate keys not allowed
    }

    root.Height = 1 + max(height(root.Left), height(root.Right))

    balance := getBalance(root)

    // Left Left Case
    if balance > 1 && data < root.Left.Data {
        return rotateRight(root)
    }

    // Right Right Case
    if balance < -1 && data > root.Right.Data {
        return rotateLeft(root)
    }

    // Left Right Case
    if balance > 1 && data > root.Left.Data {
        root.Left = rotateLeft(root.Left)
        return rotateRight(root)
    }

    // Right Left Case
    if balance < -1 && data < root.Right.Data {
        root.Right = rotateRight(root.Right)
        return rotateLeft(root)
    }

    return root
}

func inorder(root *AVLNode) {
    if root != nil {
        inorder(root.Left)
        fmt.Printf("%d ", root.Data)
        inorder(root.Right)
    }
}

func main() {
    var root *AVLNode
    keys := []int{10, 20, 30, 40, 50, 25}

    for _, key := range keys {
        root = insert(root, key)
    }

    fmt.Println("Inorder traversal of AVL tree:")
    inorder(root)
}

In this example, we implement an AVL tree in Go.
The AVLNode struct represents each node in the AVL tree, with fields for data, height, left child, and right child.
The insert function recursively inserts nodes into the AVL tree while maintaining balance using rotation operations.
The rotateLeft and rotateRight functions perform left and right rotations, respectively.
The getBalance function calculates the balance factor of a node.
We perform an inorder traversal of the AVL tree to print its elements in sorted order.

Red-Black tree

				
					package main

import "fmt"

const (
    red   = true
    black = false
)

type RBNode struct {
    Data   int
    Color  bool // red or black
    Left   *RBNode
    Right  *RBNode
    Parent *RBNode
}

type RedBlackTree struct {
    root *RBNode
}

func NewRedBlackTree() *RedBlackTree {
    return &RedBlackTree{}
}

func (t *RedBlackTree) Insert(data int) {
    if t.root == nil {
        t.root = &RBNode{Data: data, Color: black}
    } else {
        t.root = t.insertRecursive(t.root, data)
        t.root.Color = black // Ensure root is black
    }
}

func (t *RedBlackTree) insertRecursive(root *RBNode, data int) *RBNode {
    if root == nil {
        return &RBNode{Data: data, Color: red}
    }

    if data < root.Data {
        root.Left = t.insertRecursive(root.Left, data)
        root.Left.Parent = root
    } else if data > root.Data {
        root.Right = t.insertRecursive(root.Right, data)
        root.Right.Parent = root
    }

    if isRed(root.Right) && !isRed(root.Left) {
        root = t.rotateLeft(root)
    }
    if isRed(root.Left) && isRed(root.Left.Left) {
        root = t.rotateRight(root)
    }
    if isRed(root.Left) && isRed(root.Right) {
        t.flipColors(root)
    }

    return root
}

func (t *RedBlackTree) rotateLeft(node *RBNode) *RBNode {
    rightChild := node.Right
    node.Right = rightChild.Left
    if rightChild.Left != nil {
        rightChild.Left.Parent = node
    }
    rightChild.Parent = node.Parent
    if node.Parent == nil {
        t.root = rightChild
    } else if node == node.Parent.Left {
        node.Parent.Left = rightChild
    } else {
        node.Parent.Right = rightChild
    }
    rightChild.Left = node
    node.Parent = rightChild
    return rightChild
}

func (t *RedBlackTree) rotateRight(node *RBNode) *RBNode {
    leftChild := node.Left
    node.Left = leftChild.Right
    if leftChild.Right != nil {
        leftChild.Right.Parent = node
    }
    leftChild.Parent = node.Parent
    if node.Parent == nil {
        t.root = leftChild
    } else if node == node.Parent.Right {
        node.Parent.Right = leftChild
    } else {
        node.Parent.Left = leftChild
    }
    leftChild.Right = node
    node.Parent = leftChild
    return leftChild
}

func (t *RedBlackTree) flipColors(node *RBNode) {
    node.Color = !node.Color
    node.Left.Color = !node.Left.Color
    node.Right.Color = !node.Right.Color
}

func isRed(node *RBNode) bool {
    if node == nil {
        return false
    }
    return node.Color == red
}

func (t *RedBlackTree) InOrder() {
    t.inOrderTraversal(t.root)
    fmt.Println()
}

func (t *RedBlackTree) inOrderTraversal(node *RBNode) {
    if node == nil {
        return
    }
    t.inOrderTraversal(node.Left)
    fmt.Printf("(%d, %v) ", node.Data, node.Color)
    t.inOrderTraversal(node.Right)
}

func main() {
    tree := NewRedBlackTree()
    keys := []int{10, 20, 30, 40, 50, 25}

    for _, key := range keys {
        tree.Insert(key)
    }

    fmt.Println("InOrder traversal of Red-Black tree:")
    tree.InOrder()
}

In this code, we define a RBNode struct to represent each node in the Red-Black tree. Each node has data, color (red or black), left child, right child, and parent.
We define a RedBlackTree struct to represent the Red-Black tree. It contains a reference to the root node.
The Insert method inserts a new node into the Red-Black tree while maintaining its properties.
The rotateLeft and rotateRight methods perform left and right rotations, respectively, to maintain balance.
The flipColors method flips the colors of nodes to satisfy Red-Black tree properties.
The InOrder method performs an inorder traversal of the Red-Black tree, printing the nodes in sorted order along with their colors.
In the main function, we create a Red-Black tree and insert keys into it. Then, we perform an inorder traversal to display the elements in sorted order along with their colors.

Heap

				
					package main

import (
    "container/heap"
    "fmt"
)

func main() {
    // Min heap example
    h := &MinHeap{2, 1, 5, 4, 3}
    heap.Init(h)
    fmt.Println("Min Heap:")
    for h.Len() > 0 {
        fmt.Printf("%d ", heap.Pop(h))
    }
}

// MinHeap implements heap.Interface for a min-heap of int.
type MinHeap []int

func (h MinHeap) Len() int           { return len(h) }
func (h MinHeap) Less(i, j int) bool { return h[i] < h[j] }
func (h MinHeap) Swap(i, j int)      { h[i], h[j] = h[j], h[i] }

func (h *MinHeap) Push(x interface{}) {
    *h = append(*h, x.(int))
}

func (h *MinHeap) Pop() interface{} {
    old := *h
    n := len(old)
    x := old[n-1]
    *h = old[0 : n-1]
    return x
}

We define a MinHeap type that implements the heap.Interface methods for a min-heap of integers.
In the main function, we create a min heap, initialize it, and then pop elements from it, demonstrating how a min heap works.

Trie (Prefix Tree)

				
					package main

import "fmt"

type TrieNode struct {
    Children [26]*TrieNode
    IsEnd    bool
}

func main() {
    // Creating a Trie
    root := &TrieNode{}

    // Inserting keys into the Trie
    keys := []string{"hello", "world", "hi", "hey"}
    for _, key := range keys {
        insert(root, key)
    }

    // Searching for keys in the Trie
    fmt.Println("Trie Search:")
    fmt.Println(search(root, "hello")) // true
    fmt.Println(search(root, "hey"))   // true
    fmt.Println(search(root, "test"))  // false
}

func insert(root *TrieNode, key string) {
    node := root
    for _, ch := range key {
        idx := ch - 'a'
        if node.Children[idx] == nil {
            node.Children[idx] = &TrieNode{}
        }
        node = node.Children[idx]
    }
    node.IsEnd = true
}

func search(root *TrieNode, key string) bool {
    node := root
    for _, ch := range key {
        idx := ch - 'a'
        if node.Children[idx] == nil {
            return false
        }
        node = node.Children[idx]
    }
    return node != nil && node.IsEnd
}

We define a TrieNode struct representing each node in the trie, with an array of 26 children nodes to represent each character in the alphabet.
We implement insert and search functions to insert keys into the trie and search for keys, respectively.
In the main function, we create a trie, insert keys into it, and then search for keys to demonstrate how a trie works.

In this comprehensive guide, we explored various types of trees, including binary trees, binary search trees, heaps, and tries, with examples implemented in Go. Understanding these tree types and their implementations is essential for building efficient data structures and algorithms in Go. Experimenting with different tree structures and algorithms will deepen your understanding and enhance your skills as a Go developer. Happy coding !❤️

Trees in Go

What are Trees?

Binary Trees

Tree Terminology

Types of Trees

Binary Search Trees (BST)

AVL Trees

Red-Black Trees

Heap

Trie (Prefix Tree)

Implementations and Examples

Binary Tree

Binary Search Tree (BST)

AVL Tree

Red-Black tree

Heap

Trie (Prefix Tree)

Table of Contents

Explore

Popular Tutorials

Contact here