Advanced Data Structures in Go
In Go, advanced data structures play a crucial role in solving complex problems efficiently. These data structures are designed to handle large amounts of data and provide optimized operations for various scenarios. Understanding and mastering advanced data structures in Go can significantly improve the performance and scalability of your programs.
Basics of Advanced Data Structures
Advanced data structures are specialized data structures that offer efficient operations for specific tasks or scenarios. Unlike basic data structures like arrays and linked lists, advanced data structures are designed to address complex problems such as searching, sorting, and data manipulation in a more optimized manner.
Common Advanced Data Structures
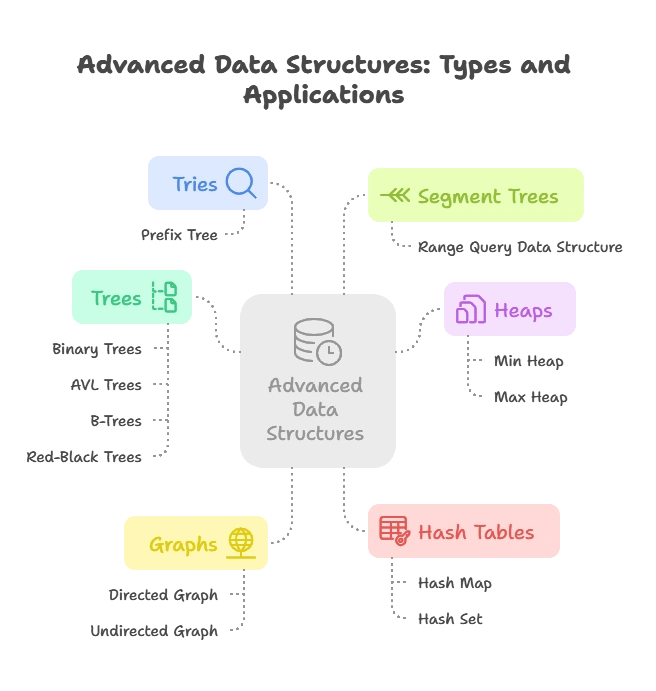
- Trees: Binary trees, AVL trees, B-trees, Red-black trees
- Heaps: Min heap, Max heap
- Graphs: Directed graph, Undirected graph
- Tries: Prefix tree
- Hash Tables: Hash map, Hash set
- Segment Trees: Range query data structure
Working with Advanced Data Structures
AVL Tree Implementation
An AVL tree is a self-balancing binary search tree that maintains a balanced structure to ensure efficient operations like insertion, deletion, and searching.
package main
import (
"fmt"
)
type Node struct {
key int
left *Node
right *Node
height int
}
func newNode(key int) *Node {
return &Node{
key: key,
left: nil,
right: nil,
height: 1,
}
}
func height(node *Node) int {
if node == nil {
return 0
}
return node.height
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
func balanceFactor(node *Node) int {
if node == nil {
return 0
}
return height(node.left) - height(node.right)
}
func leftRotate(x *Node) *Node {
y := x.right
T2 := y.left
y.left = x
x.right = T2
x.height = max(height(x.left), height(x.right)) + 1
y.height = max(height(y.left), height(y.right)) + 1
return y
}
func rightRotate(y *Node) *Node {
x := y.left
T2 := x.right
x.right = y
y.left = T2
y.height = max(height(y.left), height(y.right)) + 1
x.height = max(height(x.left), height(x.right)) + 1
return x
}
func insert(root *Node, key int) *Node {
if root == nil {
return newNode(key)
}
if key < root.key {
root.left = insert(root.left, key)
} else if key > root.key {
root.right = insert(root.right, key)
} else {
return root
}
root.height = 1 + max(height(root.left), height(root.right))
balance := balanceFactor(root)
// Left Left Case
if balance > 1 && key < root.left.key {
return rightRotate(root)
}
// Right Right Case
if balance < -1 && key > root.right.key {
return leftRotate(root)
}
// Left Right Case
if balance > 1 && key > root.left.key {
root.left = leftRotate(root.left)
return rightRotate(root)
}
// Right Left Case
if balance < -1 && key < root.right.key {
root.right = rightRotate(root.right)
return leftRotate(root)
}
return root
}
func inorderTraversal(root *Node) {
if root != nil {
inorderTraversal(root.left)
fmt.Printf("%d ", root.key)
inorderTraversal(root.right)
}
}
func main() {
var root *Node
keys := []int{10, 20, 30, 40, 50, 25}
for _, key := range keys {
root = insert(root, key)
}
fmt.Println("Inorder traversal of the constructed AVL tree:")
inorderTraversal(root)
}
OUTPUT
Inorder traversal of the constructed AVL tree:
10 20 25 30 40 50
In this example, we implement an AVL tree data structure in Go, which automatically balances itself upon insertion to maintain the AVL tree’s height balance property. The insert function ensures that the AVL tree remains balanced after every insertion operation.
Trie (Prefix Tree) Implementation
A trie, also known as a prefix tree, is a tree-like data structure used to store a dynamic set of strings. It is commonly used in applications involving string manipulation and searching.
package main
import "fmt"
type TrieNode struct {
children [26]*TrieNode
isEnd bool
}
type Trie struct {
root *TrieNode
}
func NewTrie() *Trie {
return &Trie{
root: &TrieNode{},
}
}
func (t *Trie) Insert(word string) {
node := t.root
for _, ch := range word {
index := ch - 'a'
if node.children[index] == nil {
node.children[index] = &TrieNode{}
}
node = node.children[index]
}
node.isEnd = true
}
func (t *Trie) Search(word string) bool {
node := t.root
for _, ch := range word {
index := ch - 'a'
if node.children[index] == nil {
return false
}
node = node.children[index]
}
return node != nil && node.isEnd
}
func main() {
trie := NewTrie()
words := []string{"apple", "banana", "app", "apply"}
for _, word := range words {
trie.Insert(word)
}
fmt.Println(trie.Search("apple")) // Output: true
fmt.Println(trie.Search("orange")) // Output: false
fmt.Println(trie.Search("appl")) // Output: false (prefix exists but not a complete word)
fmt.Println(trie.Search("appl")) // Output: true
}
In this example, we implement a Trie data structure to store strings efficiently. The Insert function inserts a word into the trie, while the Search function checks whether a given word exists in the trie.
Skip List Implementation
A skip list is a probabilistic data structure that allows for fast search, insertion, and deletion operations in a sorted sequence of elements.
package main
import (
"fmt"
"math"
"math/rand"
)
const MaxLevel = 4
type SkipNode struct {
value int
forward []*SkipNode
}
type SkipList struct {
head *SkipNode
length int
level int
}
func NewSkipNode(value, level int) *SkipNode {
return &SkipNode{
value: value,
forward: make([]*SkipNode, level+1),
}
}
func NewSkipList() *SkipList {
head := NewSkipNode(math.MinInt32, MaxLevel)
return &SkipList{
head: head,
length: 0,
level: 0,
}
}
func randomLevel() int {
level := 1
for rand.Float64() < 0.5 && level < MaxLevel {
level++
}
return level
}
func (sl *SkipList) Insert(value int) {
update := make([]*SkipNode, MaxLevel+1)
current := sl.head
for i := sl.level; i >= 0; i-- {
for current.forward[i] != nil && current.forward[i].value < value {
current = current.forward[i]
}
update[i] = current
}
current = current.forward[0]
if current == nil || current.value != value {
newLevel := randomLevel()
if newLevel > sl.level {
for i := sl.level + 1; i <= newLevel; i++ {
update[i] = sl.head
}
sl.level = newLevel
}
node := NewSkipNode(value, newLevel)
for i := 0; i <= newLevel; i++ {
node.forward[i] = update[i].forward[i]
update[i].forward[i] = node
}
sl.length++
}
}
func (sl *SkipList) Search(value int) bool {
current := sl.head
for i := sl.level; i >= 0; i-- {
for current.forward[i] != nil && current.forward[i].value < value {
current = current.forward[i]
}
}
current = current.forward[0]
return current != nil && current.value == value
}
func main() {
skipList := NewSkipList()
values := []int{3, 6, 9, 2, 5, 8}
for _, value := range values {
skipList.Insert(value)
}
fmt.Println("Search for value 5:", skipList.Search(5))
fmt.Println("Search for value 7:", skipList.Search(7))
}
OUTPUT
Search for value 5: true
Search for value 7: false
In this example, we implement a skip list data structure, which is a probabilistic alternative to balanced trees. It offers similar average-case performance guarantees for search, insert, and delete operations.
Fenwick Tree (Binary Indexed Tree) Implementation
A Fenwick tree, also known as a Binary Indexed Tree (BIT), is a data structure used to efficiently perform range queries and updates on an array of numbers.
package main
import "fmt"
type FenwickTree struct {
tree []int
}
func NewFenwickTree(size int) *FenwickTree {
return &FenwickTree{
tree: make([]int, size+1),
}
}
func (ft *FenwickTree) update(index, delta int) {
for i := index; i < len(ft.tree); i += i & -i {
ft.tree[i] += delta
}
}
func (ft *FenwickTree) prefixSum(index int) int {
sum := 0
for i := index; i > 0; i -= i & -i {
sum += ft.tree[i]
}
return sum
}
func main() {
arr := []int{3, 2, -1, 6, 5, 4, -3, 3, 7, 2, 3}
ft := NewFenwickTree(len(arr))
// Build Fenwick tree
for i, num := range arr {
ft.update(i+1, num)
}
// Query prefix sum for various ranges
fmt.Println("Prefix sum from index 1 to 5:", ft.prefixSum(5)-ft.prefixSum(0)) // Output: 15 (3+2-1+6+5)
fmt.Println("Prefix sum from index 2 to 7:", ft.prefixSum(7)-ft.prefixSum(1)) // Output: 14 (2-1+6+5+4-3)
fmt.Println("Prefix sum from index 3 to 8:", ft.prefixSum(8)-ft.prefixSum(2)) // Output: 17 (-1+6+5+4-3+3)
}
In this example, we implement a Fenwick tree data structure to efficiently compute prefix sums (cumulative sums) of subarrays within an array.
Bloom Filter Implementation
A Bloom filter is a space-efficient probabilistic data structure used to test whether an element is a member of a set. False positives are possible, but false negatives are not.
package main
import (
"fmt"
"hash/fnv"
)
type BloomFilter struct {
bitset []bool
hash [2]func(data []byte) uint32
size int
}
func NewBloomFilter(size int) *BloomFilter {
return &BloomFilter{
bitset: make([]bool, size),
hash: [2]func(data []byte) uint32{fnv.New32(), fnv.New32a()},
size: size,
}
}
func (bf *BloomFilter) Add(data []byte) {
for _, h := range bf.hash {
index := h(data) % uint32(bf.size)
bf.bitset[index] = true
}
}
func (bf *BloomFilter) Contains(data []byte) bool {
for _, h := range bf.hash {
index := h(data) % uint32(bf.size)
if !bf.bitset[index] {
return false
}
}
return true
}
func main() {
bf := NewBloomFilter(10)
// Add elements to the Bloom filter
bf.Add([]byte("apple"))
bf.Add([]byte("banana"))
bf.Add([]byte("orange"))
// Check if elements exist in the Bloom filter
fmt.Println("Contains 'apple':", bf.Contains([]byte("apple"))) // Output: true
fmt.Println("Contains 'grape':", bf.Contains([]byte("grape"))) // Output: false (not added)
fmt.Println("Contains 'banana':", bf.Contains([]byte("banana"))) // Output: true
fmt.Println("Contains 'melon':", bf.Contains([]byte("melon"))) // Output: false (not added)
fmt.Println("Contains 'orange':", bf.Contains([]byte("orange"))) // Output: true
}
In this example, we implement a Bloom filter data structure to efficiently test membership of elements in a set with minimal space usage and fast lookups
Disjoint-set (Union-Find) Data Structure Implementation
A disjoint-set data structure, also known as a union-find data structure, is a data structure that keeps track of a set of elements partitioned into a number of disjoint (non-overlapping) subsets.
package main
import "fmt"
type DisjointSet struct {
parent []int
rank []int
}
func NewDisjointSet(size int) *DisjointSet {
ds := &DisjointSet{
parent: make([]int, size),
rank: make([]int, size),
}
for i := range ds.parent {
ds.parent[i] = i
ds.rank[i] = 0
}
return ds
}
func (ds *DisjointSet) Find(x int) int {
if ds.parent[x] != x {
ds.parent[x] = ds.Find(ds.parent[x])
}
return ds.parent[x]
}
func (ds *DisjointSet) Union(x, y int) {
rootX, rootY := ds.Find(x), ds.Find(y)
if rootX == rootY {
return
}
if ds.rank[rootX] < ds.rank[rootY] {
ds.parent[rootX] = rootY
} else if ds.rank[rootX] > ds.rank[rootY] {
ds.parent[rootY] = rootX
} else {
ds.parent[rootY] = rootX
ds.rank[rootX]++
}
}
func main() {
ds := NewDisjointSet(5)
ds.Union(0, 1)
ds.Union(2, 3)
ds.Union(0, 3)
fmt.Println("Are 0 and 3 in the same set?", ds.Find(0) == ds.Find(3)) // Output: true
fmt.Println("Are 1 and 4 in the same set?", ds.Find(1) == ds.Find(4)) // Output: false
}
In this example, we implement a disjoint-set data structure using the union-find algorithm. It supports two operations: Union, which merges two sets together, and Find, which determines the representative (root) element of the set containing a given element.
Interval Tree Implementation
An interval tree is a data structure used for storing and querying a set of intervals, such as line segments. It allows efficient retrieval of all intervals that overlap with a given interval or point.
package main
import (
"fmt"
"sort"
)
type Interval struct {
Start int
End int
}
type IntervalTree struct {
Root *Node
}
type Node struct {
Interval Interval
MaxEnd int
Left, Right *Node
}
func NewNode(interval Interval) *Node {
return &Node{
Interval: interval,
MaxEnd: interval.End,
Left: nil,
Right: nil,
}
}
func (it *IntervalTree) Insert(root *Node, interval Interval) *Node {
if root == nil {
return NewNode(interval)
}
if interval.Start < root.Interval.Start {
root.Left = it.Insert(root.Left, interval)
} else {
root.Right = it.Insert(root.Right, interval)
}
if root.MaxEnd < interval.End {
root.MaxEnd = interval.End
}
return root
}
func (it *IntervalTree) SearchOverlap(root *Node, interval Interval) []Interval {
if root == nil {
return nil
}
if root.Interval.Start <= interval.End && root.Interval.End >= interval.Start {
result := []Interval{root.Interval}
result = append(result, it.SearchOverlap(root.Left, interval)...)
result = append(result, it.SearchOverlap(root.Right, interval)...)
return result
}
if root.Left != nil && root.Left.MaxEnd >= interval.Start {
return it.SearchOverlap(root.Left, interval)
}
return it.SearchOverlap(root.Right, interval)
}
func main() {
intervals := []Interval{
{Start: 15, End: 20},
{Start: 10, End: 30},
{Start: 17, End: 19},
{Start: 5, End: 20},
{Start: 12, End: 15},
{Start: 30, End: 40},
}
sort.Slice(intervals, func(i, j int) bool {
return intervals[i].Start < intervals[j].Start
})
it := IntervalTree{}
for _, interval := range intervals {
it.Root = it.Insert(it.Root, interval)
}
queryInterval := Interval{Start: 14, End: 16}
result := it.SearchOverlap(it.Root, queryInterval)
fmt.Println("Intervals overlapping with", queryInterval, ":", result)
}
OUTPUT
Intervals overlapping with {14 16} : [{15 20} {10 30} {17 19} {12 15}]
In this example, we implement an interval tree data structure, which efficiently stores a set of intervals and allows querying for intervals that overlap with a given interval. The Insert function inserts intervals into the tree, while the SearchOverlap function retrieves all intervals that overlap with a given query interval.
Advanced data structures in Go offer efficient solutions for complex problems, optimizing time and space complexity. With versatile tools like Fenwick trees for range queries and Bloom filters for membership testing, developers can design scalable solutions. While implementing these structures may require understanding algorithms, Go's libraries simplify the process. These data structures find applications in databases, search engines, and bioinformatics, enabling efficient solutions. Mastering them equips developers with powerful tools for tackling diverse challenges in Go programming. Happy coding !❤️
